A new Financial Stability Paper from the Bank of England offers some re-assurance about the adequacy of the ‘cover 2’ standard for the default fund of central counterparties. It also suggests, though, that supervisors should monitor the distribution of tail risks to ensure that it remains adequate.
The paper, by David Murphy and Paul Nahai-Williamson, begins with the definition of the cover 2 standard: systemically important clearing houses “must have sufficient financial resources to … be robust under the failure of … their two largest members in extreme but plausible circumstances.” The authors observe that this standard is unusual, because it makes no reference to the total number of members involved.
Thus, as they write ”adding new clearing member risk to a CCP does not necessarily increase the risk to be covered by the default fund” unless the increase contributes one of those two worst-loss scenarios.
For any scenario, the pertinent loss is that which remains after the initial margin is subtracted. So the report details matrixes of “stressed losses over IMs,” or SLOIMs. The pronunciation of the acronym is unspecified, but I have to hope it would rhyme with “homes.”
Here is an example of such a matrix, adapted a bit from the paper’s Table B.
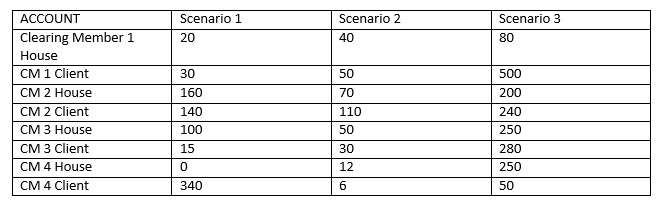
There are a number of conceptual issues with ‘cover 2.’ For example: does it involve two literally simultaneous events? Two events that come within the same week? The same year? Or is there some other specifiable measuring period? Murphy and Nahai-Williamson observe that regulators often require after a loss from one default that a CCP refill its default fund within a specified time frame. For most leading CCPs, the refill period required is “rather short,” that is, refill is often accomplished within a week or less.
Unfortunately, “there no direct market-based estimates of the probability of multiple defaults in short periods of time.” Thus, some modeling is necessary here.
But let us get back to the issue of the consequence for risk as the number of members of a particular clearing house increases. First: the probability of two or more failures among the members (a key to the cover 2 standard of course) will increase as there are more members: that is, a house with 20 members is less likely to see two of them fail in a particular period than is a house with 70 members.
On the Other Hand
Second, though, the probability that a two-independent-defaults event will involve the biggest two decreases as the number of members decreases as total membership increases. So the bad event that the house must be prepared to cover becomes less likely.
One key turn in the analysis in the B of E paper is the authors’ introduction of the matter of risk distribution. There are three cases to consider: that risk is concentrated in a small group of the CMs – they say that this is “often found in practice”; that all members contribute the same amount of risk (not commonplace); and that “a single large clearing member accounts for a significant proportion of the total SLOIM” (also not commonplace.) The second and third possibilities are “edge cases,” considered in order to convey an idea of the range of possibilities.
To be more specific about the third possibility, which the authors call the “whale” distribution, they suppose 30 members of a CH. One member accounts for 40% of SLOIM, and the SLOIMs of the other embers follow an exponential distribution downward.
After some further discussion, the authors conclude that for both the first and the third of the possibilities just listed, “the robustness of cover 2 … falls rapidly as membership increases from four members to around fifteen members; but thereafter is little changed as membership increases.” After what one might call the equilibrium size of 15 members, the two consequences of further increases balance one another out, and the cover 2 requirement as a proportion of the total SLOIM remains constant up to 70 members.
OTOH, the mathematics for the edge case of “flat distribution” (all members contributing the same risk) is more worrisome. There is no equilibrium, the proportion of cover total as against total SLOIM continues to drop as membership increases until (at least) 60 members.
The over-all conclusion of the study is that cover 2 “is a prudent standard for the risk distributions likely to be found in practice,” but that CCPs themselves and their supervisors ought to continue to monitor loss distribution, and reconsider cover 2 should distributions start to approximate this flatness. That would require “higher levels of financial resources … to ensure clearing house robustness.”