By Giulio Renzi-Ricci, Senior Investment Strategist, Vanguard
Investor interest in private equity has been rising over the last two decades. Today private equity represents a growing opportunity for multiasset portfolios, offering the potential to significantly outperform public investments. In a new research paper, we examine the role private equity can play in a strategic, long-term portfolio and introduce a new portfolio construction framework that accounts for private equity's unique risk and return characteristics.
Asset allocation models: Key input, assumptions, and objectives
Traditional asset allocation models are built based on modern portfolio theory (MPT). Popular approaches among asset managers, such as the Black-Litterman model, allow them to incorporate active views and are constructed using the same methodological framework of mean-variance optimization as specified by Markowitz in the 1950s. Asset allocation models built using this approach need a series of specific inputs, often derived from a risk model that ultimately provides a forward-looking estimate on: 1) the expected level of returns for each asset of the multiasset portfolio, 2) the level of volatility for each of these assets, and 3) their pairwise correlations. In addition to predicting returns, volatilities, and correlations, asset allocation models require an estimate for the level of risk tolerance that must be consistent with the investment’s objective and time horizon. In utility-based optimization approaches,1 this means estimating a risk aversion coefficient, whereas in standard mean-variance analysis, the risk tolerance is implied by the desired level of expected volatility of the portfolio.
Also, multiasset optimization models often allow the user to set relative and absolute constraints on assets’ weights to avoid the risk that the model chooses extreme asset allocations (i.e., corner solutions), which would not be prudent for the asset owner. More importantly, asset allocation models are normally built with liquid assets in mind, assuming the portfolio can be rebalanced periodically, as the assets under consideration can be bought or sold easily. However, when a portfolio includes illiquid investments such as private equity, some methodological changes are required in the model to take into account the key differences associated with private equity—frictionless rebalancing being only one of them.
Key differences between private and public equity investing
Those who invest in private equity tend to believe its portfolio benefits outweigh its unique challenges—challenges that publicly traded liquid assets do not entail. Although private equity shares some common sources of risk and return with public equity, there are four key structural differences to consider when deciding whether to include it in a diversified portfolio:
- Smoothed (appraisal-based) private equity return estimates: Private equity historical return data have limited holdings transparency and are based on subjective appraisal-based valuations rather than observable, transaction-based prices on a public exchange. Relying solely on appraisal-based values to calculate returns can lead to significant underestimation of the volatility of returns.
- Illiquidity and frictionless rebalancing: Investors in private equity have less ability to trade their investment and rebalance their portfolio back to the intended target allocation. For this reason, they should require compensation in the form of a liquidity premium.
- Uncertainty in timing and magnitude of cash flows: Because private equity investors cannot control the timing or size of private equity fund cash flows, they incur an additional type of risk.
- Illiquidity and valuation adjustment: Private equity fund investments cannot easily be accessed and liquidated unless at a discount to NAV in most cases. This implies that liquid asset prices and private equity fund NAVs are not directly comparable.
Given these challenges, how should investors build multiasset portfolios that include private equity as well as traditional and liquid asset classes?
Building multiasset portfolios with private equity
Conventional asset allocation approaches such as mean-variance optimization usually omit liquidity and active risk dimensions of the risk-return trade-off. We introduce a new portfolio construction framework that accounts for private equity’s unique risk and return characteristics and embed it into our proprietary model, the Vanguard Asset Allocation Model (VAAM). VAAM solves these challenges by determining asset allocation among passive, active, and factor investments simultaneously. It makes allocation decisions by adopting a utility-based optimization framework that seeks to maximize the expected utility of wealth (Aliaga-Díaz et al., 2019). The important differences between private equity and public market investments highlighted previously create challenges for incorporating private investments into an asset allocation model like VAAM. Accounting for and modeling these differences is critical for a sensible portfolio construction framework that can be extended to illiquid investments. Four main adjustments to the standard framework are needed:
- Estimating unbiased private equity returns
Historical return data for private equity tend to have limited transparency and rely on subjective, appraisal-based valuations. Applying standard asset-pricing statistical techniques developed for public performance data can therefore lead to unreliable and misleading results. A number of statistical methods have been proposed in the academic literature over the last few decades to try to better understand historical performance. In our research, we follow a time-series technique to “unsmooth” reported private equity returns. The use of “smooth” appraisal-based private equity valuations would result in underestimating the fund’s equity market beta and volatility of returns, leading to an overestimation of its risk-adjusted performance. More specifically, we use an econometric approach by using a Geltner (1993) method to transform the time series from reported (smoothed) returns to an estimate of marked-to-market (unsmoothed) returns. As Figure 1 shows, this approach provides for more economically sensible volatility and covariance estimations while preserving the average return of the private equity investments.
Figure 1. Unsmoothing private equity returns results in a more realistic economic return profile
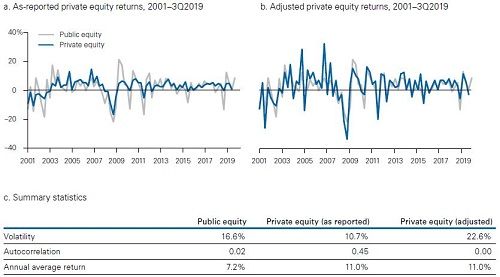
Notes: The time series of private equity returns is based on global, pooled, quarterly net returns to limited partners for venture capital and buyout direct funds from the Burgiss Manager Universe for the period December 31, 2001, to September 30, 2019. The public equity returns are based on the MSCI All Country World Index. The Modified Dietz returns produced by Burgiss are unsmoothed using a Geltner (1993) method, which allows us to remove first-order autocorrelation from the return series to create the adjusted results.
Sources: Vanguard calculations, using Burgiss and Morningstar, Inc.
- Model illiquidity-constrained portfolio rebalancing (dropping the frictionless rebalancing assumption)
The standard assumption in most portfolio construction frameworks of frictionless and periodic rebalancing is invalid for illiquid assets such as private equity. Ang, Papanikolaou, and Westerfield (2014) account for the drift in the illiquid asset allocation (akin to a buy-and-hold strategy) when full frictionless rebalancing is not possible and the illiquid asset cannot be traded for an uncertain period of time. Following a similar approach, we model an illiquidity constraint that prevents full rebalancing of private equity in our asset allocation model. This illiquidity-constrained rebalance feature provides a more accurate representation of the risk-return trade-offs between liquidity premium and risks associated with private equity assessed within the portfolio optimization. It also allows for the derivation of key portfolio analytics to assess illiquidity risks in the portfolio, such as the probability of breaching an investor’s maximum private equity threshold.
- Explicitly modeling private equity cash flows
Investors are exposed to funding liquidity risk because distributions and capital calls are decided by the private equity fund manager. On the distributions side, payments at unknown times would tend to push the portfolio toward being underallocated over time. On the capital calls side, the uncertain schedule of the drawdowns means that the risk of being overallocated at any point in time is significant. Private equity cash flows introduce an additional decision of how to invest them, unlike reinvestment features of some liquid investments. Although commitments to new vintages or matching capital calls with distributions may provide some hedge to this risk, they cannot eliminate the risk of significant misallocation at any point in time. Explicitly modeling cash flows in a multiasset portfolio with private equity is therefore important, along with estimating the cash flow ex ante uncertainty and relevant rebalancing rules.
- Optional valuation adjustment of the illiquid wealth of the portfolio
The capital invested in private equity is inaccessible to the investor for an extended period of time, unless through the secondary market, but at a discount to NAV in most cases. Thus, it may be appropriate to account for the disparity between the market value of liquid and illiquid assets in the portfolio at the end of the investment horizon. We add this valuation adjustment feature to our model. Similar to Hayes, Primbs, and Chiquoine (2015), we account for the liquidity disparity between private and public assets by specifying a discounting factor, applied to private equity wealth in the portfolio. In other words, we assume that once the portfolio is valued at the end of the investment horizon, private equity is assessed at market prices (e.g., in the secondary market), usually at a discount to the appraisal-determined fund NAV. The discount function effectively converts illiquid wealth into its liquid equivalent. Incorporating these features into an asset allocation model allows us to analyze several practical examples of private equity allocations. Figure 2 shows a few examples of the asset allocation for a portfolio with a medium level of active risk aversion.2
Figure 2. Model-derived private equity allocations for policy portfolios with medium active risk aversion
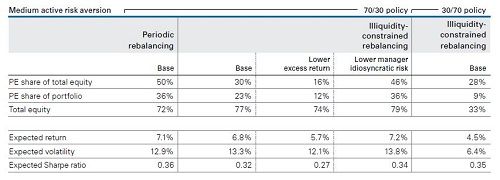
Notes: Expected return, expected volatility, and expected Sharpe ratio are median values from a distribution of 10,000 simulations. Portfolios have been optimized over a 10-year investment horizon. The following constraints apply: non-U.S. bonds, up to 50% of total (noncredit) bonds; total credit bonds, up to 50% of total fixed income (bonds and credit bonds); intermediate-term U.S. credit bonds, up to 60% of total credit bonds; short-term U.S. credit bonds, up to 60% of total credit bonds. For these case studies, we assume that the only sub-asset class in the portfolio with active investments is private equity. For the illiquidity-constrained rebalancing portfolios, a 15% NAV discount rate was assumed on the private equity wealth at the end of the 10-year investment horizon. The base case portfolios refer to the standard equity/bond mix policy portfolios, whereas the lower excess return and lower manager idiosyncratic risk portfolios refer to sensitivity testing portfolios.
Source: Vanguard calculations, using asset-return projections as of December 31, 2019, in USD. IMPORTANT: The projections and other information generated by the VCMM regarding the likelihood of various investment outcomes are hypothetical in nature, do not reflect actual investment results, and are not guarantees of future results. Distribution of return outcomes from VCMM are derived from 10,000 simulations for each modeled asset class. Simulations as of December 31, 2019. Results from the model may vary with each use and over time.
The results show how a 70/30 equity/bond policy portfolio that ignores private equity's illiquid characteristics (no valuation adjustment and frictionless rebalancing to target) leads to a higher allocation in private equity compared with our enhanced framework, which takes into account illiquidity risks. More specifically, the private equity share within equities decreases substantially, dropping from 50% to 30%. Consistent with previous research findings, lower manager’s alpha expectations or lower manager’s idiosyncratic risk leads to a lower (12% vs. 23%) and higher (36% vs. 23%) allocation to private equity, respectively. For the 30/70 equity/bond portfolio, although the total equity allocation decreases significantly in line with the more conservative policy, the target private equity share of total equity does not change materially relative to that of the 70/30 investor. In other words, for higher passive risk aversion levels, the weight of private equity decreases proportionally compared to the weight of total equity allocation.3
In summary, portfolio analyses and simulations using our framework and allocation model demonstrate that private equity can play a significant role in strategic, long-term, diversified portfolios. There is no single recommended allocation for all eligible investors. Private equity allocations depend on each investor’s specific set of circumstances, such as the degree of risk tolerance, including active risk tolerance, and the ability to find and access high-quality managers. Most importantly, using standard asset allocation models that do not reflect the unique aspects of illiquid assets may lead to an unintended overallocation to private equity, bringing with it unintended risks. In our paper, we present some of those unique aspects of illiquid assets and illustrate how to incorporate them into an asset allocation framework.
References
Aliaga-Díaz, Roger, Giulio Renzi-Ricci, Ankul Daga, and Harshdeep Ahluwalia, 2019. Vanguard Asset Allocation Model: An Investment Solution for Active-Passive-Factor Portfolios. Valley Forge, Pa.
Ang, Andrew, Bingxu Chen, William N. Goetzmann, and Ludovic Phalippou, 2018. Estimating Private Equity Returns From Limited Partner Cash Flows. The Journal of Finance 73(4): 1751–1783.
Geltner, David M., 1993. Estimating Market Values From Appraised Values Without Assuming an Efficient Market. Journal of Real Estate Research 8(3): 325–345.
Hayes, Mark, James A. Primbs, and Ben Chiquoine, 2015. A Penalty Cost Approach to Strategic Asset Allocation With Illiquid Asset Classes. The Journal of Portfolio Management 4(2): 33–41.
End notes:
1 Expected utility maximization approaches face the objective of maximizing the expected utility of wealth at the end of the investment horizon. Typical utility functions used in these cases assume constant relative risk aversion. Mean-variance optimization and expected utility optimization are closely related. Mean-variance optimization is consistent with an expected utility approach that assumes a quadratic utility function. More generally, mean-variance can be considered a first degree approximation of other expected utility optimization approaches.
2 For further details on the optimal allocation between active and passive refer to Aliaga-Díaz et al. (2019). For further details and the underlying inputs used for Figure 2, refer to Aliaga-Díaz, Roger, Giulio Renzi-Ricci, Harshdeep Ahluwalia, Douglas M. Grim, and Chris Tidmore, 2020. The Role of Private Equity in Strategic Portfolios. Valley Forge, Pa.: The Vanguard Group.
3 In general, a tradeoff between “alpha” allocations and “beta” exposures is typical of VAAM active-passive portfolios. When a high-information-ratio active asset (here given by the private equity performance assumptions) is introduced as an investment option, both the active-passive mix and the overall stock-bond split are impacted.
Disclosures: IMPORTANT: The projections and other information generated by the Vanguard Capital Markets Model regarding the likelihood of various investment outcomes are hypothetical in nature, do not reflect actual investment results, and are not guarantees of future results. VCMM results will vary with each use and over time. The VCMM projections are based on a statistical analysis of historical data. Future returns may behave differently from the historical patterns captured in the VCMM. More important, the VCMM may be underestimating extreme negative scenarios unobserved in the historical period on which the model estimation is based. The Vanguard Capital Markets Model® is a proprietary financial simulation tool developed and maintained by Vanguard’s primary investment research and advice teams. The model forecasts distributions of future returns for a wide array of broad asset classes. Those asset classes include U.S. and international equity markets, several maturities of the U.S. Treasury and corporate fixed income markets, international fixed income markets, U.S. money markets, commodities, and certain alternative investment strategies. The theoretical and empirical foundation for the Vanguard Capital Markets Model is that the returns of various asset classes reflect the compensation investors require for bearing different types of systematic risk (beta). At the core of the model are estimates of the dynamic statistical relationship between risk factors and asset returns, obtained from statistical analysis based on available monthly financial and economic data from as early as 1960. Using a system of estimated equations, the model then applies a Monte Carlo simulation method to project the estimated interrelationships among risk factors and asset classes as well as uncertainty and randomness over time. The model generates a large set of simulated outcomes for each asset class over several time horizons. Forecasts are obtained by computing measures of central tendency in these simulations. Results produced by the tool will vary with each use and over time. All investing is subject to risk, including the possible loss of the money you invest. Diversification does not ensure a profit or protect against a loss. Private investments involve a high degree of risk and therefore, should be undertaken only by prospective investors capable of evaluating and bearing the risks such an investment represents. Investors in private equity generally must meet certain minimum financial qualifications that may make it unsuitable for specific market participants. Private equity investments are speculative in nature and may lose value. © 2020 The Vanguard Group, Inc. All rights reserved.
Interested in contributing to Portfolio for the Future? Drop us a line at content@caia.org




